Deux types d'activités : (1) "Conférences" -- (2) "Maths à Modeler"
mais aussi un atelier au Printemps des Sciences

Activités proposées (1)

Nous proposons une composante spécifique du type "conférence". Les sujets traités permettent entre autres de montrer que des théorèmes a priori purement théoriques peuvent trouver des applications parfois inattendues. Ainsi un des objectifs poursuivis (mais pas le seul !) est de répondre modestement à une question maintes fois posée :

Les maths, ça sert à quoi ?
Pour répondre par l'exemple, un théorème dû à Fermat au début du XVII siècle et traitant de théorie des nombres est utilisé quotidiennement pour sécuriser des millions de transactions électroniques sur Internet. Ou encore, un théorème d'algèbre linéaire dû à Perron et datant du début du siècle passé est à la base de moteurs de recherche comme Google.

Une autre approche, proposée par Pierre Lecomte, professeur au Département de Mathématiques de l'ULg, est d'éclairer des sujets de géométrie sous un angle différent. Elle permet d'apporter une certaine réflexion sortant du cursus classique abordé dans l'enseignement secondaire.

Ce genre d'activités, par son regard décalé par rapport au cadre scolaire usuel, peut aussi déboucher sur une discussion autour des mathématiques et des métiers grands consommateurs de celles-ci (actuariat, gestion du risque, météorologie, sécurité informatique, imagerie médicale,...). Les exemples sont nombreux et, trop souvent, méconnus du grand public. Voir par exemple la brochure "Zoom sur les métiers des mathématiques".

Quelques exemples :

• Le triangle des triangles, P. Lecomte
• Triangles acutangles et tétraèdres isocèles, P. Lecomte
• Pirates informatiques et mathématique modulaire, M. Rigo (4-5-6)
• La matrice cachée de Google, M. Rigo (5-6 math. 6 heures)
• Les codes correcteurs, M. Rigo (4-5-6)
• Mathémagie, M. Rigo (4-5-6)
• Game Over : Mathématiques et jeux vidéos, M. Rigo (4-5-6)
• Qui veut jouer avec moi ?, M. Rigo (3-4-5-6)

Activités proposées (2)

Nous proposons des activités du type "Maths à Modeler" dans les établissements d'enseignement secondaire (voire primaire) en Communauté Française de Belgique (tous réseaux confondus) et ce, tout au long de l'année scolaire, ainsi que dans des foires scientifiques grand public, comme le Printemps des Sciences ou la Nuit des Chercheurs.

Il nous semble aussi intéressant de proposer l'ensemble de ces activités aux régendats et écoles normales pour sensibiliser les futurs enseignants à l'importance des Mathématiques et sur les multiples facettes de leur enseignement.



L'approche choisie pour initier aux raisonnements mathématiques est l'emploi de jeux manipulés par le public (plateaux en bois, pions, pièces de formes variées, ...). Par ce choix, elle est très attractive pour de jeunes élèves parfois peu enclins aux mathématiques. Il est par exemple possible de faire sentir l'importance de la notion de preuve en mathématiques, d'introduire naturellement le raisonnement par récurrence, de travailler sur les notions de condition nécessaire et suffisante.

En général, les intervenants de l'équipe présentent des problèmes ouverts pour lesquels les chercheurs professionnels ne connaissent pas (encore) la solution, et font travailler le public sur des cas particuliers "abordables" de ces problèmes. C'est un moyen de montrer que, contrairement à une idée reçue, les mathématiques ne sont pas une science figée et que l'activité scientifique y est grande. 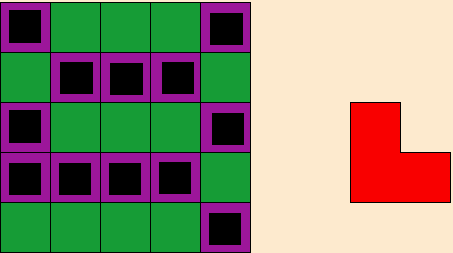L'une des situations-recherche favorites de l'équipe se nomme la chasse à la bête. Sur une quadrillage de taille 5*5, on place des "pièges" - chaque piège utilisé occupant une case de la grille - de sorte que les bêtes (qui ont une forme fixée au départ) ne puissent pas se poser sur la grille. L'objectif est de minimiser le nombre de pièges nécessaires. Sur l'exemple ci-dessous, les bêtes ont une forme de L, et nous proposons une solution avec 12 pièges. Est-il possible de faire mieux ?